Defining Explainability

Kacper Sokol

Topics

• Nomenclature
• What Is Explainability?
• Defining Explainability
• Examples
• Wrap Up

Nomenclature

Black Box

A system or automated process whose internal workings are opaque to the observer – its operation may only be traced by analysing its behaviour through its inputs and outputs

Black Box    

Sources of opaqueness:

1. a proprietary system, which may be transparent to its creators, but operates as a black box
2. a system that is too complex to be comprehend by any human

(Rudin 2019)

Black Box    

Spectrum of opaqueness determined by the context (audience, purpose, etc.)

• Instead of binary yes/no opaque, it seems more appropriate to have a continuous scale

(Sokol and Flach 2021)

Transparency, Interpretability, Explainability, …

Transparency, Interpretability, Explainability, …    

• explainability
• intelligibility
• simulatability
• sensemaking
• cause

• observability
• comprehensibility
• explicitness
• insight

• transparency
• understandability
• justification
• evidence

• explicability
• interpretability
• rationalisation
• reason

• A lot of different terms are used interchangeably

• They are (re)defined in a large number of papers

• We will try to organise this catalogue of words

What Is Explainability?

Lack of a universally accepted definition

Interpretability is the degree to which a human can understand the cause of a decision

Explanation is an answer to a “Why?” question

(Miller 2019; Biran and Cotton 2017)

Lack of a universally accepted definition    

Explanations should answer “Why?” and “Why-should?” questions until such questions can no longer be asked

(Gilpin et al. 2018)

Lack of a universally accepted definition    

Explanations “giv[e] a reason for a prediction” and answer “how a system arrives at its prediction”

Justifications “put an explanation in a context” and convey “why we should believe that the prediction is correct”

• justifications do not necessarily communicate how the system truly works

(Biran and McKeown 2014)

Lack of a universally accepted definition    

Transparency is a passive characteristic of a model that allows humans to make sense of it on different levels

Explainability is an active characteristic of a model that is achieved through actions and procedures employed (by the model) to clarify its functioning for a certain audience

(Arrieta et al. 2020)

Lack of a universally accepted definition    

Interpretability is the degree to which a human can consistently predict the model’s result

(Kim, Khanna, and Koyejo 2016)

Lack of a universally accepted definition    

Transparency is the ability of a human to comprehend the (ante-hoc) mechanism employed by a predictive model on three levels

• decomposability – appreciation of individual components (input, parameterisation and computation) that constitute a predictive system
• algorithmic transparency – understanding the modelling process embodied by a predictive algorithm
• simulatability enables humans to simulate a decisive process in vivo at the level of the entire model

(Lipton 2018)

Lack of a universally accepted definition    

Marr’s three-level hierarchy of understanding information processing devices

1. computational theory – abstract specification of the problem at hand and the overall goal.
2. representation and algorithm – implementation details and selection of an appropriate representation
3. hardware implementation – physical realisation of the explained problem

• These three tiers are only loosely related
• Some phenomena may be explained at only one or two of them
• Identify which of these levels need to be covered in each individual case to arrive at understanding

(Marr 1982)

Lack of a universally accepted definition    

Understanding why birds fly cannot be achieved by only studying their feathers:

In order to understand bird flight, we have to understand aerodynamics; only then do the structure of feathers and the different shapes of birds’ wings make sense.

Lack of a universally accepted definition    

Fidelity-based understanding

• completeness – how truthful the understanding is overall (generality)
• soundness – how accurate the understanding is for a particular phenomenon (specificity)

• Complete understanding can be applied to other domains

• The depth of understanding, i.e., the level of (over)simplification

• completeness without soundness is likely to be too broad, hence uninformative

• the opposite can be too specific to the same effect

(Kulesza et al. 2013)

Lack of a universally accepted definition    

Mental models withing the completeness–soundness landscape

• functional – operationalisation without understanding
• structural – appreciation of the underlying mechanism

• Electricity and light bulb scenario

(Kulesza et al. 2013)

Approaches to defining XML concepts

• no definition
• inherently intuitive – You know it when you see it!
• assuming terms are synonymous

Approaches to defining XML concepts    

• circular or tautological definitions

  • “something is explainable when we can interpret it”
  • “interpretability is making sense of ML models”
  • “interpretable systems are explainable if their operations can be understood by humans”
  • “intelligibility is the possibility to comprehended something”

• dictionary definitions

  • to interpret is “to explain […] the meaning of”
  • to explain is to “present in understandable terms”

Approaches to defining XML concepts    

• hierarchical and ontological definitions

  • creating a web of connections

• component-based – pairings between keywords and technical component or properties

  • data are understandable; models are transparent; predictions are explainable
  • interpretability is determined by fidelity, brevity and relevance of the insights

• hierarchies and ontologies are difficult to parse, follow and apply

Defining Explainability

Human-agnostic definitions

• (technical) desiderata of explainers
• (abstract) properties of explanations

Human-centred definitions

• the role and needs of (human) explainees
• the goal of explanations (with respect to explainees)

---

• The Chinese Room Theorem (Searle 1980)

• problem with simulatability
• replication-based definitions, more broadly

Terminology & Key Concepts

• Transparency – insight (of arbitrary complexity) into operation of a system
• Background Knowledge – implicit or explicit exogenous information encompassing (operational) context such as application area, stakeholder and audience (domain expertise)
• Reasoning – algorithmic or mental processing of information

Definition

\[ \texttt{Explainability} \; = \] \[ \underbrace{ \texttt{Reasoning} \left( \texttt{Transparency} \; | \; \texttt{Background Knowledge} \right)}_{\textit{understanding}} \]

• Explainability is a socially-grounded technology
• It provides insights that lead to understanding
• Understanding largely depends upon the explanation recipients, who come with a diverse range of background knowledge, experience, mental models and expectations (context)
• It is a process – a loop

(Sokol and Flach 2021)

Goal

Explainability → explainee walking away with understanding

• This notion both conceptualises explainability and fixes its evaluation criterion (as we will see in the next module)
• Note that it is not about task completion but understanding
• Recall The Chinese Room Argument

Understanding, explainability & transparency

A continuous spectrum rather than a binary property

• Explainability is not a binary property; it is a continuous spectrum

Examples

• transparency is different from explainability – both overcome opaqueness, but only the latter leads to understanding

Linear Models

\[ f(\mathbf{x}) = 0.2 \;\; + \;\; 0.25 \times x_1 \;\; + \;\; 0.7 \times x_4 \;\; - \;\; 0.2 \times x_5 \;\; - \;\; 0.9 \times x_7 \]

\[ \mathbf{x} = (0.4, \ldots, 1, \frac{1}{2}, \ldots \frac{1}{3}) \]

\[ f(\mathbf{x}) = 0.2 \;\; \underbrace{+0.1}_{x_1} \;\; \underbrace{+0.7}_{x_4} \;\; \underbrace{-0.1}_{x_5} \;\; \underbrace{-0.3}_{x_7} \;\; = \;\; 0.6 \]

• linear models are transparent given a reasonable number of features

• with the right ML and domain background knowledge they become explainable

  • normalised features
  • effect of feature correlation
  • meaning of features and coefficients

– the explainee can reason about their properties, leading to an explanation based on understanding - visualisation can help – refer back to XXX

Linear Models    

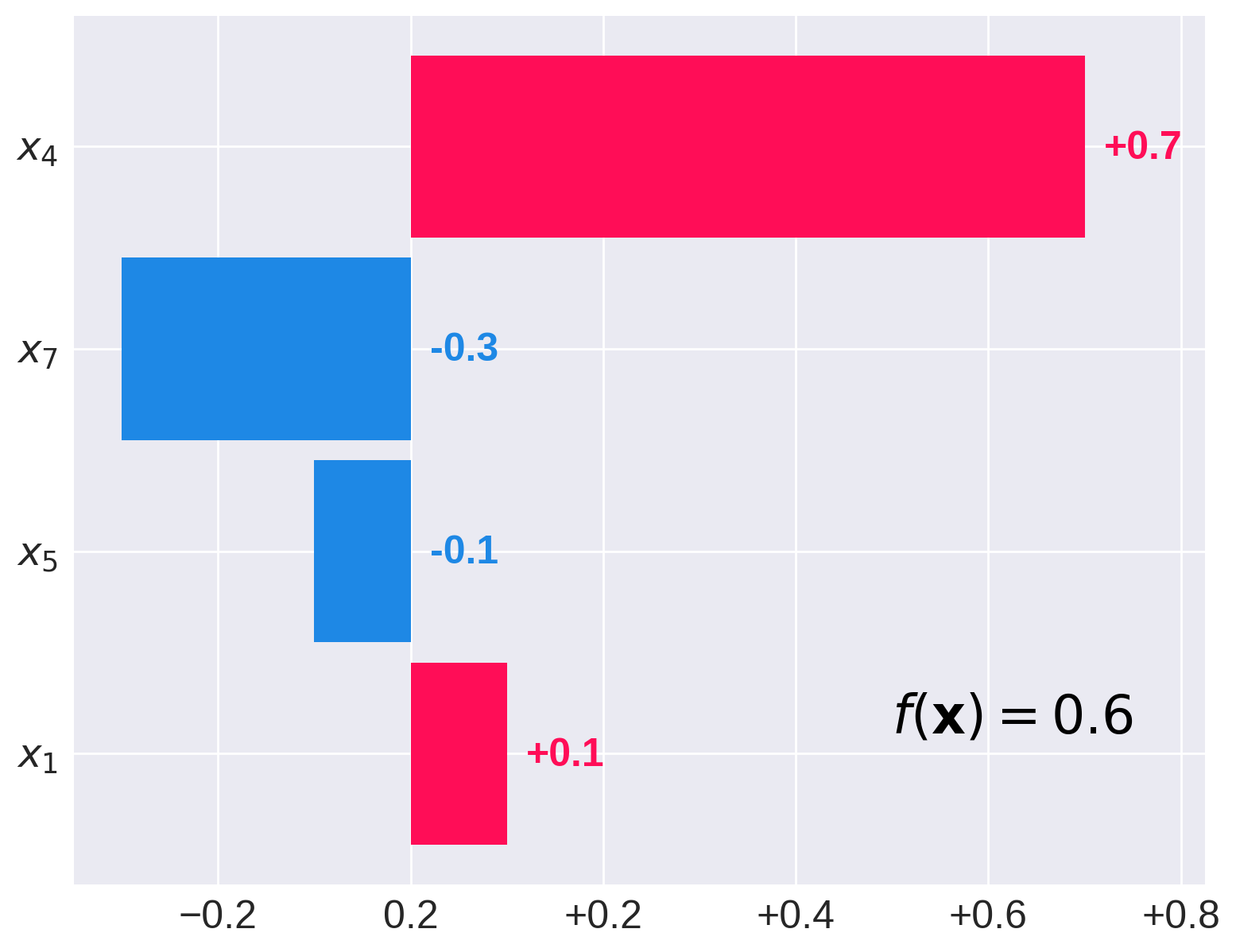
Linear Models    

Decision Trees

• visualisation of a shallow decision tree can be considered both transparent, and arguably explainable assuming that the explainee understands how to navigate its structure (ML background knowledge) and the features are meaningful (domain background knowledge);
• people were shown to believe that the feature used by the root-node split is the most important attribute (Bell et al. 2022)
• it is up to the explainee to reason about these insights

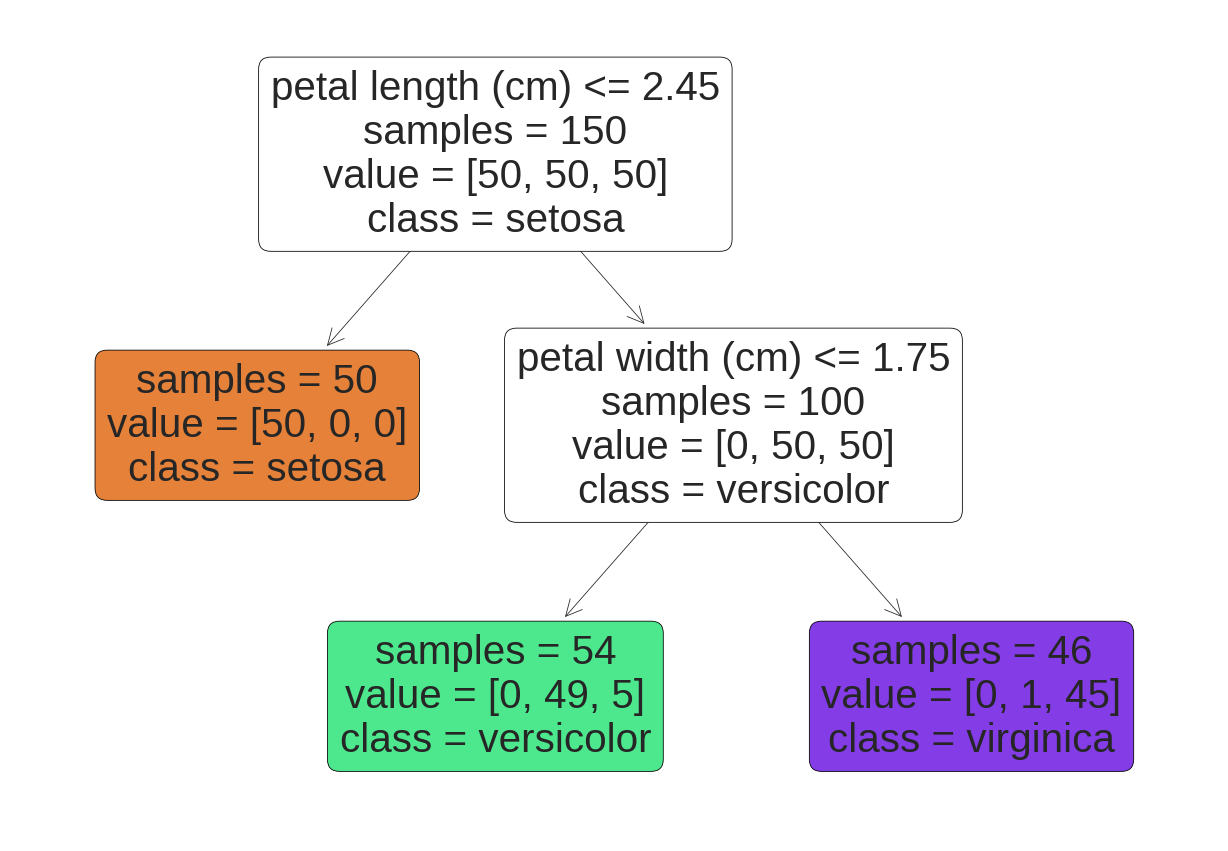
Decision Trees    

• when the size of a tree increases, its visualisation loses the explanatory power because many explainees become unable to process and reason about its structure

• restoring the explainability of a deep tree requires delegating the reasoning process to an algorithm that can digest its structure and output sought after insights in a concise representation

• for explaining a prediction, the tree structure can be traversed to identify a similar instance with a different prediction, e.g., as encoded by two neighbouring leaves with a shared parent

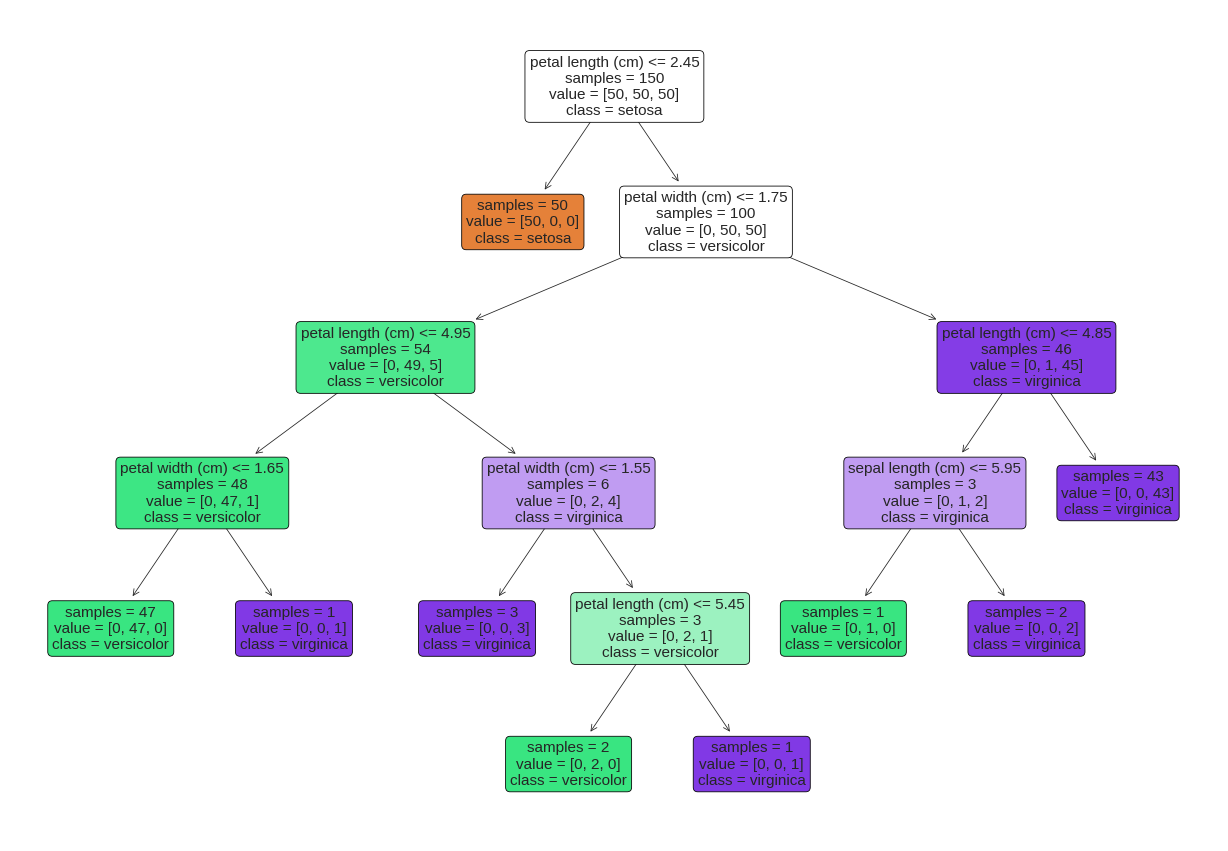
Wrap Up

Summary

• Explainability is an elusive concept
• Its definition relies on the broadly-understood context
• It should be human-centred and goal-driven
• It should lead to understanding

Bibliography

Arrieta, Alejandro Barredo, Natalia Dı́az-Rodrı́guez, Javier Del Ser, Adrien Bennetot, Siham Tabik, Alberto Barbado, Salvador Garcı́a, et al. 2020. “Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges Toward Responsible AI.” Information Fusion 58: 82–115.

Bell, Andrew, Ian Solano-Kamaiko, Oded Nov, and Julia Stoyanovich. 2022. “It’s Just Not That Simple: An Empirical Study of the Accuracy-Explainability Trade-Off in Machine Learning for Public Policy.” In 2022 ACM Conference on Fairness, Accountability, and Transparency, 248–66.

Biran, Or, and Courtenay Cotton. 2017. “Explanation and Justification in Machine Learning: A Survey.” In IJCAI-17 Workshop on Explainable AI (XAI), 8:8–13. 1.

Biran, Or, and Kathleen McKeown. 2014. “Justification Narratives for Individual Classifications.” In Proceedings of the AutoML Workshop at ICML, 2014:1–7.

Gilpin, Leilani H, David Bau, Ben Z Yuan, Ayesha Bajwa, Michael Specter, and Lalana Kagal. 2018. “Explaining Explanations: An Overview of Interpretability of Machine Learning.” In 2018 IEEE 5^th International Conference on Data Science and Advanced Analytics (DSAA), 80–89. IEEE.

Kim, Been, Rajiv Khanna, and Oluwasanmi O Koyejo. 2016. “Examples Are Not Enough, Learn to Criticize! Criticism for Interpretability.” In Advances in Neural Information Processing Systems, 2280–88.

Kulesza, Todd, Simone Stumpf, Margaret Burnett, Sherry Yang, Irwin Kwan, and Weng-Keen Wong. 2013. “Too Much, Too Little, or Just Right? Ways Explanations Impact End Users’ Mental Models.” In Visual Languages and Human-Centric Computing (VL/HCC), 2013 IEEE Symposium on, 3–10. IEEE.

Lipton, Zachary C. 2018. “The Mythos of Model Interpretability.” Communications of the ACM 16 (3): 30:31–57. https://doi.org/10.1145/3236386.3241340.

Marr, David. 1982. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. The MIT Press.

Miller, Tim. 2019. “Explanation in Artificial Intelligence: Insights from the Social Sciences.” Artificial Intelligence 267: 1–38.

Rudin, Cynthia. 2019. “Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead.” Nature Machine Intelligence 1 (5): 206–15.

Searle, John R. 1980. “Minds, Brains, and Programs.” Behavioral and Brain Sciences 3 (3): 417–24.

Sokol, Kacper, and Peter Flach. 2021. “Explainability Is in the Mind of the Beholder: Establishing the Foundations of Explainable Artificial Intelligence.” arXiv Preprint arXiv:2112.14466.

Questions

kacper.sokol@rmit.edu.au
k.sokol@bristol.ac.uk